クラスで、誕生日が同じ日になる人の確立は?
どのくらいだろうか。
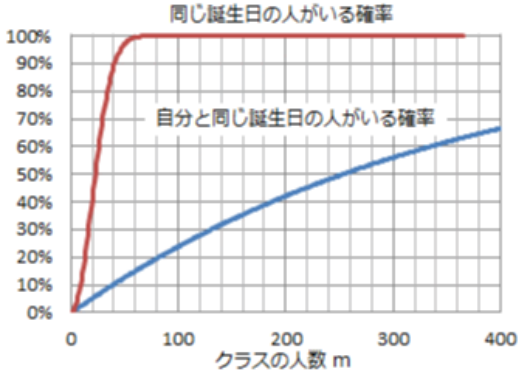
正解は、90%くらいになる!
クラスに一組は同じ誕生日の人がいる計算になります。
「これは、意外な答えだと思った」
私は、一年は365日だから、1/365で、
0.3%くらいで、低いが回答でした。
問題が、「自分と誕生日が同じになる確立は?」だったら正解でした。
では、どうやって計算するのか。
誕生日が同じになる確率は、さすがに、計算できないため、
逆にクラス(40人)の誕生日が同じにならない確率を
計算すると求められるらしいです。
クラスに同じ誕生日の人が居ない確立
まず、1人目は365日のうちどの日付でもよいので、365/365 = 1 。
つまり、1人のクラスだと誕生日が同じ人がいない確率は100%(全員の誕生日が違う)ということです。
2人目の誕生日は、1人目と違う日付です。
すなわち、2人目の誕生日は365通りのうち、
1人目の日付を除いた364通りしかありません。
そこで、「365/365 × 364/365」を計算すると、
答えは0.997。99.7%という高確率で、
2人の誕生日が違うことになります。
3人目でも同じことをして、365/365 × 364/365 × 363/365 = 0.992(99.2%)。
この調子で40人分やれば完了です。
40人分を計算すると、0.097(9.7%) まで下がります。
確かに、高確率で誕生日が同じになりますね。
そういえば、双子の誕生日は、同じだよな。
突然ですが、やぎさんのお悩み、くるりが解決します!
自分からの目線でしか みてないね! 俯瞰してみないと ですよ

